1 确定的有穷自动机 (DFA)
1 形式化定义
确定的有穷自动机 (Deterministic Finite Automata):DFA是一个五元组,如:$M=(Q,\; \Sigma,\; \delta,\;q_0,\; F)$ ,其中,
- $Q$ 是有限的状态集,包含DFA中所有的状态;
- $\Sigma$ 是有限的输入字符集,也就是DFA的字母表;
- $q_0$ 是初始状态,并且 $q_0\in Q$;
- $F$ 是终结状态的集合,并且 $F \in Q$;
- $\delta$ 是状态转移函数,它是一个映射:$Q \times \Sigma \to Q $
$\delta$ 要对 $Q$ 中所有的状态和 $\Sigma$ 中所有的状态的组合都要有定义,也就是笛卡尔积是一个单射
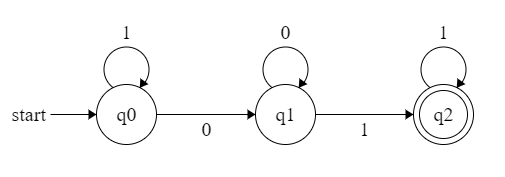
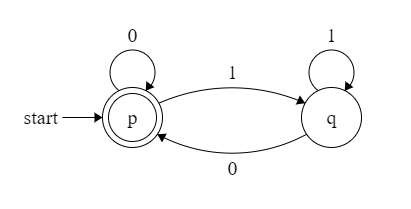
例:以自动门为例,使用 $0$ 表示关门信号,$1$ 表示开门信号,$p$ 表示关门状态,$q$ 表示开门状态,则DFA如下:
状态集:${p,\; q}$
输入字符集:${0,\;1}$
初始状态:$p$
终结状态:$p$
状态转移函数:$\delta$ \(\delta(p,\; 0)=p\\ \delta(p,\; 1)=q\\ \delta(q,\; 1)=q\\ \delta(q,\; 0)=p\) 故该DFA的定义为:${ {p,\; q},\;{0,\;1},\;\delta,\;\;p,\;{p}}$
用图表示:单线圈表示普通状态,双线圈表示终结状态,弧表示状态转移函数
用表格表示:用 $\to$ 标识出初始状态,用 $*$ 标识出终结状态
| 0 | 1 | |
|---|---|---|
| $\to*p$ | $p$ | $q$ |
| $\qquad q$ | $p$ | $q$ |
DFA的目的是区分字符串,于是,按照如上例子构造的DFA就把字符串分成了两类:
$L_1={ w\in{0,1}^* \;|\; w \; end \; with \; 0 }\cup {\,\varepsilon\,}
L_2={ w\in{0,1}^* \;|\; w \; end \; with \; 1 }$
而 $L_1$ 就是该DFA所接受的字符串集合,就能够判断任意的字符串 $w$,$w \in L_1$ 是否成立。
2 构造
构造一个DFA的一般步骤:
- $w \in L$ 指的是哪些 $w$
- 根据能够产生的字符串划分等价类
- 根据划分的等价类设置状态
- 添加状态转移
例:构造DFA接受 $L = {x01y\; |\; x\; and\; y\; are\; consists\; of\; any\; number\; of\; 0’s\; and\; 1’s }$
{ ε,0,1,00,==01==,10,11,000,==001==,==010==,100,==011==,==101==,110,111,0000,==0001==,==0010==,==0100==,1000,==0011==,==0101==,==1001==, …}
高亮的是 $L$ 应该接受的字符串
观察这些字符串,有如下发现:
没有0出现的时候,也就是都是1的时候效果是同样的,所以可以划分为一个类;
有0出现,但没有1出现的时候等待1出现就可以了,所以这不同于上一类,又可以划分为一类;
有0出现,有1出现,就有了01子串,而之后无论再出现什么都是会被接受的了,所以这是一类;
根据上面划分的3类可以设置三个状态 $q0,\;q1,\;q2$
添加状态转移得到结果:
![image-20200630212921894]()
定义:若 $ A = (Q, Σ, δ, q_0, F )$ 是一个 DFA,则 D 接受的语言为 $L(A) = {w \in Σ^∗\; |\; \hatδ(q_0, w) \in F}$ 。
3 正则语言
定义:如果存在一个DFA接受 $L$,那么就称 $L$ 是一个正则语言。这类 $L$ 就被称为正则语言。
练习:Construct DFA for following languages :
a) ${\, 0\, }^*$
b) ${\,w\; |\; w \in {0,1}^*\; and\; begin\; with\; 0\, }$
c) ${\, w\;|\; w\; consists\; of\; any\; number\; of\; 0’s\; followed\; by \;any\; number \;of \;1’s }$
d) ${\, \varepsilon\, }$
e) $\phi$
2 非确定的有穷自动机 (NFA)
形式化定义
非确定的有穷自动机 (Nondeterministic finite automaton):NFA是一个五元组,如:$M=(Q,\; \Sigma,\; \delta,\;q_0,\; F)$ ,其中,
$Q$ 是有限的状态集,包含NFA中所有的状态;
$\Sigma$ 是有限的输入字符集,也就是NFA的字母表;
$q_0$ 是初始状态,并且 $q_0\in Q$;
$F$ 是终结状态的集合,并且 $F \in Q$;
$\delta$ 是状态转移函数,它是一个映射:$Q \times \Sigma \to 2^Q $
与DFA唯一的不同就是 $\delta$ 的象集是 $Q$ 的幂集,结果是一个集合
例:构造NFA接受 $L_{x01} = { x01\; |\; x \;is \;any \;strings \;of \;0’s \;and \;1’s\, }$
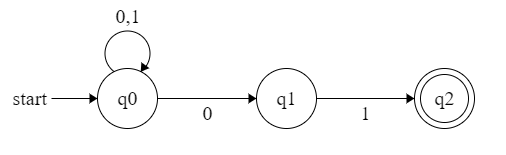
可以看到,$\delta(q0,\, 0)={q0,\,q1}$,得到的就是一个集合。
$\delta(q1,\, 0)=\phi$ 表明NFA不接受这个输入,NFA可以简化这种记法,但DFA不行。
定义:若 $A = (Q, Σ, δ, q_0, F )$ 是一个 NFA,则 D 接受的语言为 $L(A) = {w\; |\; \hatδ(q_0, w) \cap F \ne \phi\,}$ 。
只需要有一条路能够让 $w$ 从 $q_0$ 走到终结状态就可以说NFA接受 $w$。这也是为什么它是非确定的。
3 DFA和NFA的等价性
如果一个DFA和一个NFA接受的是同一个语言,那么就称这两个FA是等价的。而对于能构造一个DFA来接受它的语言来说,也必定能构造一个NFA来接受它,反之亦然。所以,所有的DFA和对应的NFA都是等价的。
证明:
显然,如果有一个DFA接受L,则必定有一个NFA接受L;
给定一个DFA:$A=(Q_D,\;\Sigma,\;\delta_D,\; q_0,\;F_D)$,构造一个对应的NFA:$B= (Q_N,\;\Sigma,\;\delta_N,\;q_0,\;F_N)$
则 $Q_N=Q_D$, $\delta_N(q, a)={\delta_D(q,\, a)}$ , $F_N=F_D$。
再证,如果有一个NFA接受L,则必定有一个DFA接受L。
给定一个NFA:$A= (Q_N,\;\Sigma,\;\delta_N ,\; q_0,\;F_N)$,构造一个对应的DFA:$B=(Q_D,\;\Sigma,\;\delta_D,\;q_0,\;F_D)$
令 $Q_D=2^{Q_N}={S\; | \;S \subseteq Q_N}$
则 $\delta_D(S,\, a) = \bigcup\limits_{p\in S}\delta_N(p,\,a)$,因为$S$ 是 $Q_N$ 的一个子集,所以把 $S$ 中的每个元素在 $a$ 下确定状态后合并即可。
则 $F_D={S\;|\;S\subseteq Q_N \;and \;S\cap F_N \ne \phi}$。注:显然 $F_D$有可能不仅有一个元素。
例:用上一节 (2) 中 $L_{x01}$ 的例子来看,NFA已经构造好了,用已有的NFA构造DFA如下:
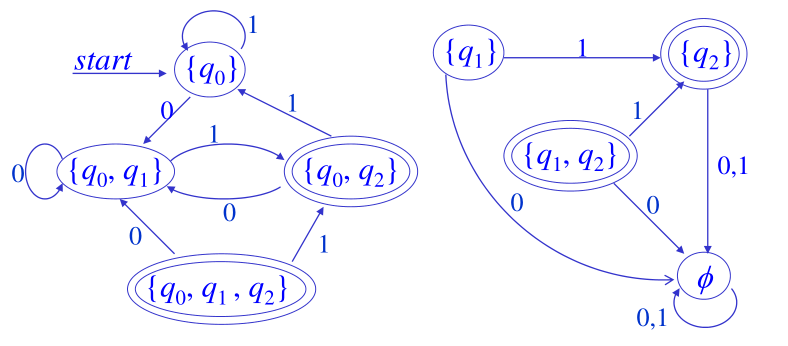
图中可以看出左半部分的 ${q_0,\,q_1,\,q_2}$ 这个状态显然是不可达的,没有意义,可以删去,右半部分同理也可删去。就简化成了如下的样子:
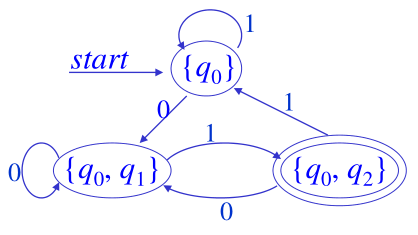
转化的另一个办法,子集构造法(Sub-set construction),惰性计算,走一步看一步,较上面的办法清爽许多。基本过程是从初始状态开始,看它可能走到哪些状态,然后看它走到的状态又分别能走到哪些状态,如此循环直到没有新的状态出现。
还是用上面的例子做说明:
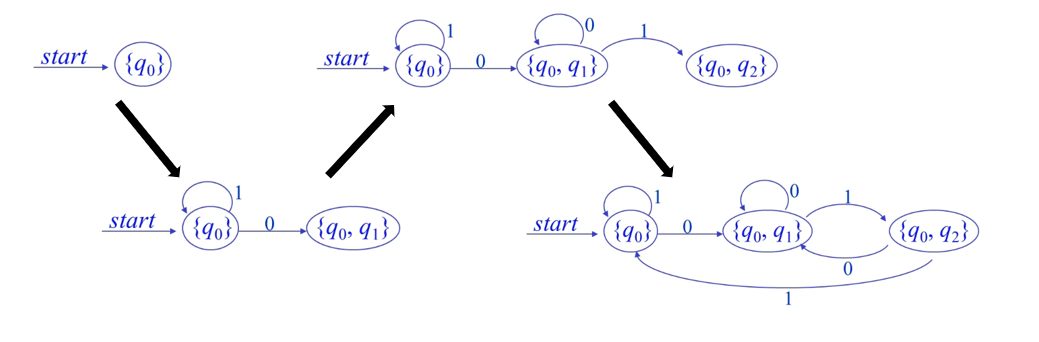
解题方法:因为NFA的行为更接近于人的思维,所以构造DFA的题可以先构造NFA然后转化成DFA
4 ε-NFA和最小化DFA
1 ε-NFA的形式化定义
带有空转移的非确定有穷自动机:ε-NFA是一个五元组,如:$M=(Q,\; \Sigma,\; \delta,\;q_0,\; F)$ ,其中,
$Q$ 是有限的状态集,包含NFA中所有的状态;
$\Sigma$ 是有限的输入字符集,也就是NFA的字母表;
$q_0$ 是初始状态,并且 $q_0\in Q$;
$F$ 是终结状态的集合,并且 $F \in Q$;
$\delta$ 是状态转移函数,它是一个映射:$Q \times {\Sigma \cup {\varepsilon}} \to 2^Q $
与NFA唯一的不同在于 $\delta$ 多了一个 $\varepsilon$ 输入 ,因而多了一个空转移行为。
2 ε-闭包
ε-闭包:状态q可以通过 (一次或多次) ε空转移到达的状态构成的集合就是q的ε-闭包,记为ECLOSE(q),或更简单的E(q)。自己到自己也是空转移!!!例:
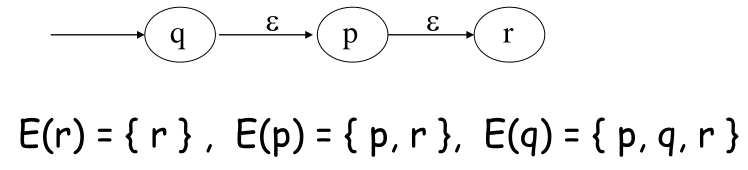
在状态 $q$ 读了字符串 $w $ 可以到达的状态:
NFA:$\hat\delta(q,\, w)={\,p_1,\, p_2,\, …,\, p_k\,}$
ε-NFA:$\hat\delta(q,\, w)=\bigcup\limits_{i=1}^m E(r_i)$
定义:若 $A = (Q, Σ, δ, q_0, F )$ 是一个 ε-NFA,则 D 接受的语言为 $L(A) = {w\; |\; \hatδ(q_0, w) \cap F \ne \phi\,}$ 。
其实和NFA接受的语言是一样的
3 DFA的最小化问题
最小化DFA就是找到一个等价的状态数最少的DFA
对于两个状态,一定是 等价 / 可区分 的。
等价:$\forall w \in \Sigma^*,\, \hat\delta(p,\, w)\in F \Leftrightarrow \hat\delta(q,\, w)\in F$
注意:表明的是对于一个输入,两个状态都转移到终结状态或都转移到非终结状态,并不一定相同!
可区分:$\exist w\in \Sigma^*,\, \hat\delta(p,\, w)\in F \Leftrightarrow \neg \hat\delta(q,\, w)\in F $
当两个状态为可区分时,存在至少一个输入符,转移后状态不都为终结状态或不都为非终结状态。
例:
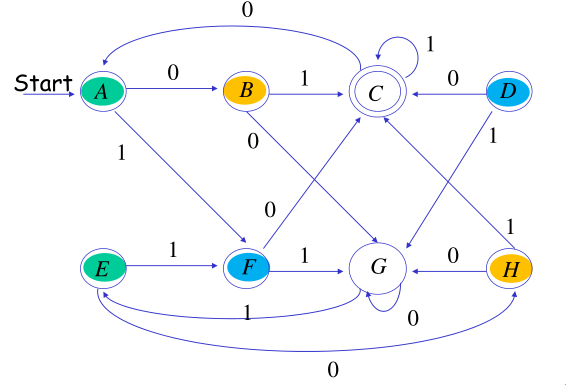
—— Table-filling algorithm ——-
把所有的状态对画成一张表,逐个检查所有的状态对,如果可区分,则把该格子标记,直到填完,剩下的没有标记的格子就是不可区分(等价)的状态对。
判断两个状态对可区分的策略:
- 终结状态和非终结状态一定是可区分的
- 两个状态读相同的字符,一个到了终结状态,一个到了非终结状态,则是可区分的
所以,要找让一个状态到终结状态的输入串,看在这个串下另一个状态是不是到了非终结状态,如果是就能很快判断了。
上例用 Table-filling algorithm 得到的结果:
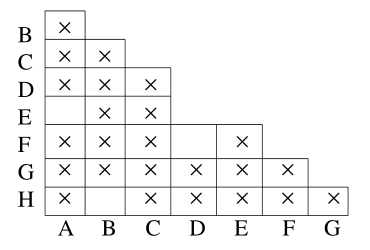
最后把等价的状态捏在一起就好了,就得到了最小化后的DFA。