1 正则表达式
正则表达式的递归定义:
- $\varepsilon$ 是一个正则表达式,表示语言 ${\varepsilon}$ ;
- $\phi$ 是一个正则表达式,表示空语言 $\phi$ ;
- $\forall a \in \Sigma$,$a$ 是一个正则表达式, 表示语言 ${a}$ ;
- 如果 $E$ 和 $F$ 是正则表达式,表示的语言分别是 $L(E)$ 和 $L(F)$,则 $E+F,\;EF,\;E^$ 都是正则表达式,分别表示的语言是 $L(E)\cup L(F),\; L(E)L(F),\;(L(E))^$ ;
- 如果 $E$ 是正则表达式,则 $(E)$ 也是。
运算符优先级:括号 > 星 > 连接 > 加
每一个正则表达式都对应一个正则语言。
例:$L={w\; |\; w \in { 0, 1 }^* \;and \;w \;has \;no \;pair \;of \;consecutive \;0’s }$
解:$1^* ( 0 1 1^* )^* ( 0 + \varepsilon)$ 或 $(1+01)^*(0 + \varepsilon)$
练习:RegExp for ($\Sigma={0,1}$)
- {w | w has exactly a single 1 }
- {w | w contains 001 }
- {w | length(w) ≥ 3 and the third symbol is 0 }
- What language does the RegExp $\phi^*$ represent ?
2 正则表达式和FA的等价性
1 等价性
- 有穷自动机可以识别正则语言
- 正则表达式可以生成正则语言
- 故 有穷自动机和正则表达式等价
2 正则表达式$\Rightarrow$FA
正则表达式三种运算的转换:通过空转移
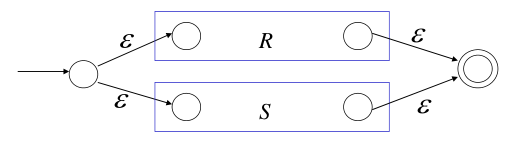
加:R+S
![image-20200703115520917]()
连接:RS
![image-20200703115532654]()
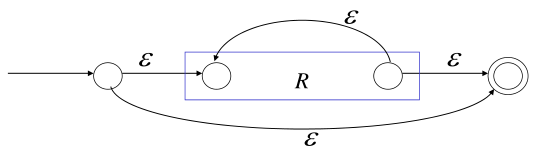
星:R*
![image-20200703115552947]()
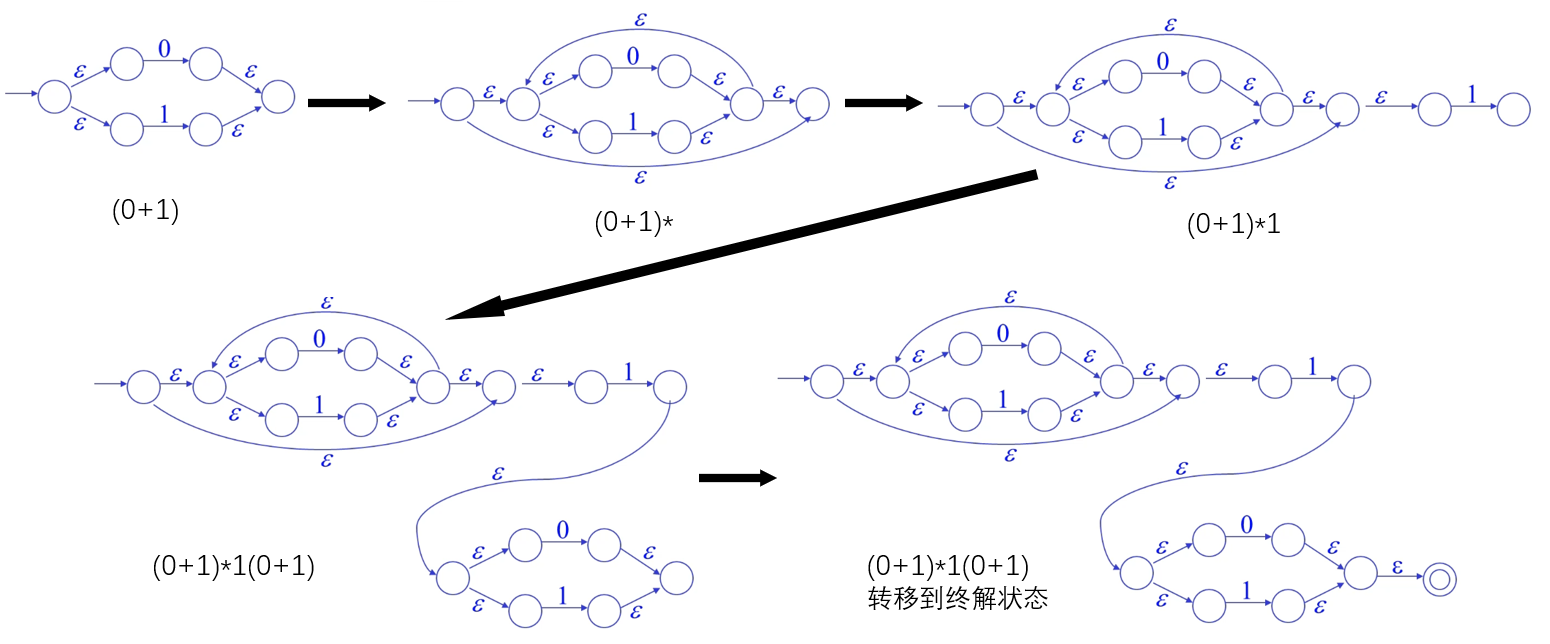
例:将 (0+1)*1(0+1) 转化为FA
3 FA$\Rightarrow$正则表达式
一些题目可以直接“看“出来,像这样:
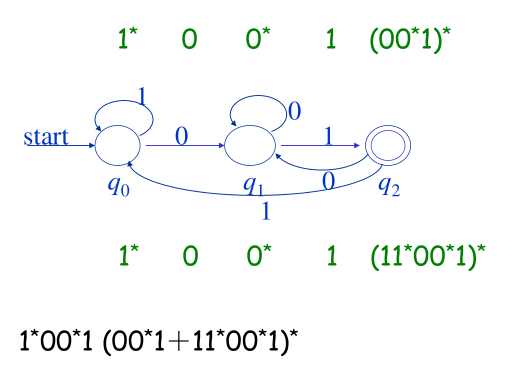
但是题目太复杂了,容易丢三落四,于是使用状态消去法。过程如下:

然后每次消去一个状态,并将该状态表示的表达式添加在弧上
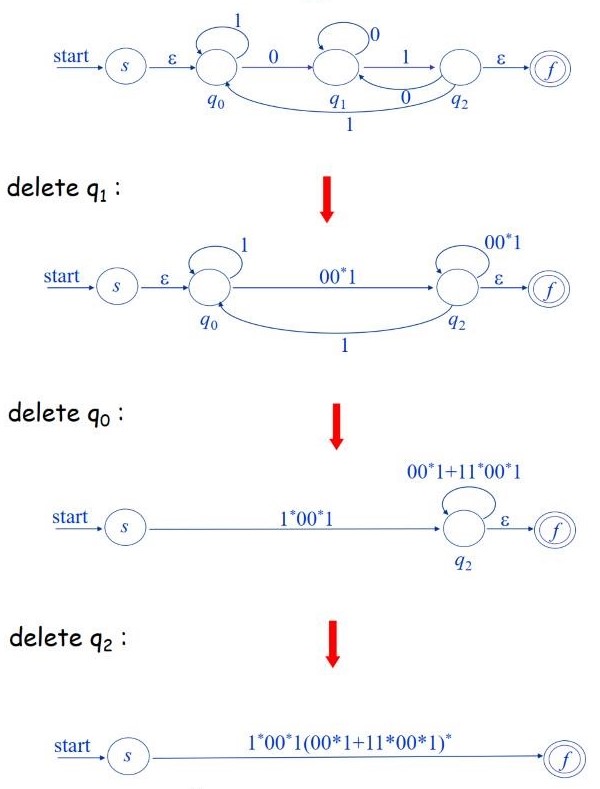
最后弧上得到的表达式就是该FA对应的正则表达式。
**归纳法**将状态标记为 Q={1, 2, 3, ……, n}
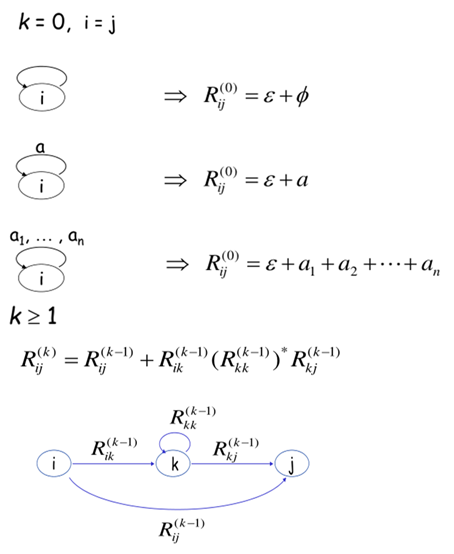
$R_{ij}^{(k)}\;其中0 \le k \le n$:i 到 j 路径的正则表达式,且路径上没有标记超过 k 的状态
过程:按照k=0,i=j 的公式算出不经过中间状态的正则表达式,然后递推套k≥1的公式就行。
3 正则语言的性质
1 泵引理 (Pumping lemma)
泵引理用于证明某个语言不是正则的,它是正则语言应满足的必要条件
要证明是正则的可以使用构造DFA、NFA、ε-NFA、正则表达式的方法
正则语言的泵引理:假设 L 的是正则的,则 $\exists n$,对 $\forall w \in L$,若$|w|\ge n $,则可将 w 划分为 $w=xyz$,其中
- $|xy|\le n$
- $y \ne \varepsilon (|y|\ge 1)$
- $\forall k\ge 0,\, xy^kz \in L$
例:证明 $L={0^n1^n \, | \, n\ge 0}$ 不是正则的
解:假设它是正则的。由泵引理可知,一定存在一个常数n,对每个长度不小于n的$w\in L$,可以被分成3的子串 $w=xyz$,且$|xy|\le n$,$y \ne \varepsilon$,$xy^kz \in L$
取 $w=0^n1^n \in L$,则 $w=0^n1^n=xyz$,由于$|xy|\le n$,故只能有 $y=0^m$,所以有 $xz=0^{n-|y|}1^n \in L$。
显然xz不是L中的字符串,所以矛盾,所以L不是正则的。
解题方法:上手先假设L是正则的,根据泵引理,选一个字符串w (最好是在开始的某个字符上重复了n次,即最开始是一个 $a^n$),然后就可以泵掉 |y| 个 a,然后就不属于L了,就推出矛盾
2 封闭性
正则语言经某些运算后得到的新语言仍是正则语言,称正则语言在这些运算下封闭。
- 并:$L \cup M$
- 交:$L\cap M$
- 补:$\overline L$
- 差:$L - M$
- 反:$L^R$
- 闭包(星):$L^*$
- 连接:$LM$
- 同态:$h:\; \Sigma^* \rightarrow \Gamma^*\qquad h(L)={ h(w)\, |\, w \in L }$
- 逆同态