1 上下文无关文法 (CFG)
1 形式化定义
上下文无关文法 (Context-Free Grammars):CFG是一个四元组,如:$G=(V,T,S,P)$,其中
- $V$:变元的集合,是一个有限集;(变量)
- $T$:终结符的集合,是一个有限集,且 $V \cap T = \phi$;(值)
- $S$:开始变元,$S \in V$;
- $P$:产生式的集合,是一个有穷集,其中的每个元素都有形式:$A \rightarrow \alpha$,其中 $A \in V, \alpha \in (V \cup T)^*$
派生:由产生式生成字符串的过程。
最左派生:每次选取派生式的最左的变元派生替换。
最右派生:每次选取派生式的最右变元派生替换。
例如:$L=\{a^{2n}b^m | n \ge 0, m \ge 0 \}$ 的产生式为:$S\rightarrow AB,\, A\rightarrow \varepsilon | aaA,\, B\rightarrow \varepsilon | Bb$
对于字符串 $w=aabb$ 来说,派生式如下:
$S\Rightarrow AB \Rightarrow aaAB \Rightarrow aaABb \Rightarrow aaBb \Rightarrow aaBbb \Rightarrow aabb$
最左派生:$S\Rightarrow AB\Rightarrow aaAB\Rightarrow aaB\Rightarrow aaBb\Rightarrow aaBbb \Rightarrow aabb$
最右派生:$S\Rightarrow AB\Rightarrow ABb\Rightarrow ABbb\Rightarrow Abb\Rightarrow aaAbb\Rightarrow aabb$
上下文无关语言 (CFL):$G=(V,T,S,P)$ 是一个CFG,则 $L(G)=\{w\;|\;w\in T^* \; and\; S \stackrel{*} {\Longrightarrow} w\}$
2 语法分析树
语法分析树:$G=(V,T,S,P)$ 是一个CFG,一个G的语法分析树如下:
- 每个内节点都标了一个 $V$ 中的变元;
- 每个叶节点都标了一个 $T\cup \{\varepsilon\}$ 中的符号,所有被 ε 标记的叶节点都是其父节点的唯一子节点;
- 如果一个内节点标记为A,它的子节点(从左到右)标记为 $x_1,x_2, …, x_k$,则 $A\rightarrow x_1,x_2, …, x_k \in P$
例:$L=\{ w\; |\; w\in \{0,1\}^*\; and\; w = w^R \}$ 产生式为 $S \rightarrow \varepsilon\, |\, 0\, |\, 1\, |\, 0S0\, |\, 1S1$ 两个语法分析树如下:
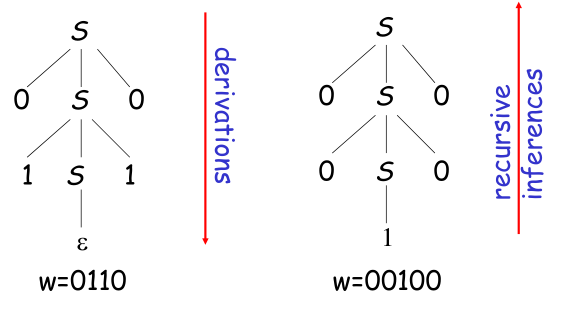
3 二义性
对于一个CFG:$G=(\{E,I\}, \{a, b, (, ), +, \}, E, P)$,产生式为 $E\rightarrow I\; |\; E+E |\;EE\;|\;(E)$,$ I\rightarrow a\;|\;b$
对于字符串 $w=a+a*a$ 的两种最左派生如下:
$E\Rightarrow EE\Rightarrow E+EE\Rightarrow I+EE\Rightarrow a+EE\Rightarrow a+aa
E\Rightarrow E+E\Rightarrow I+E\Rightarrow a+E\Rightarrow a+EE\Rightarrow a+a*a$
对应的语法分析树如下,发现一个先算的是加法,一个先算的是乘法,出现了歧义。
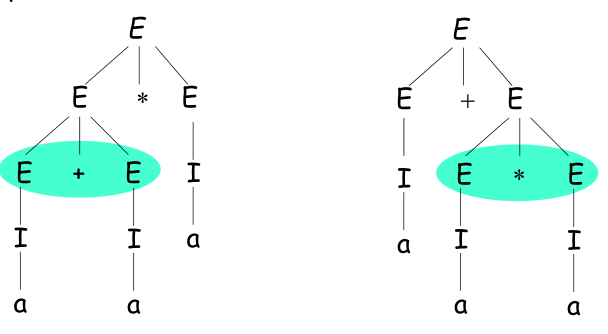
重新构造产生式以消除歧义:
先算乘法的:$E\rightarrow I\; |\; E+E\; |\; E*E\; |\; (E),\; I\rightarrow a\; |\; b$
先算加法的:$E\rightarrow T\; |\; E+T,\; T\rightarrow F\; |\; T*F,\; F\rightarrow I\; |\;(E),\; I\rightarrow a\;|\;b\;|\;Ia\;|\;Ib$
定义同样的语言可以有多个文法,如果一个CFL的所有文法都是歧义的,那么它是固有二义性的
4 CFG的化简
- 去掉 ε 产生式;
- 去掉单元产生式;
- 去掉无用的产生式;
5 乔姆斯基范式(CNF)
乔姆斯基范式(Chomsky Normal Form):一个CFG的所有的产生式都有如下两种形式之一:
- $A\rightarrow BC$,$A,B,C\in V$
- $A\rightarrow a$,$a\in T$
CFG可以转换为CNF的形式,如下例子。
例:将 $S\rightarrow ABa , A\rightarrow aab , B \rightarrow Ac$ 转化为CNF的形式
解:$S\rightarrow AC,A\rightarrow DE,B\rightarrow AF,C\rightarrow BD,D\rightarrow a,F\rightarrow c,E\rightarrow DG,G\rightarrow b$
2 下推自动机(PDA)
由于FA有局限性,可以识别$M=\{0^n1^m | n \ge 0, m \ge 0 \}$,但不能识别$L=\{ 0^n1^n | n \ge 0 \}$,所以有了PDA
1 形式化定义
下推自动机(Pushdown Automata):PDA是一个七元组$P=(Q,\,\Sigma,\,\Gamma,\,\delta,\,q_0,\,z_0,\,F)$,其中,
- $Q$ 是有限的状态集;
- $\Sigma$ 是有限的输入字符集;
- $\Gamma$ 是有限的栈字符集;
- $\delta$ 是状态转移函数,是一个映射 $Q\times (\Sigma\cup\{\varepsilon\})\times \Gamma \Rightarrow 2^Q\times \Gamma^*$;
- $q_0$ 是初始状态;
- $z_0$ 是初始栈符,表示栈是空的;
- $F$ 是终结状态集;
例:构造PDA识别 $L=\{ww^R|w\in\{0,1\}^*\}$
解:第一步,把 $w$ 入栈 \(\delta(q,0,z_0)=(q,0z_0),\quad \delta(q,1,z_0)=(q,1z_0)\\ \delta(q,0,0)=(q,00),\quad \delta(q,1,0)=(q,10)\\ \delta(q,0,1)=(q,01),\quad \delta(q,1,1)=(q,11)\) 第二步,从栈中弹出 $w^R$ \(\delta(q,1,1)=(p,\varepsilon),\quad \delta(q,0,0)=(q,\varepsilon)\\ \delta(p,1,1)=(p,\varepsilon),\quad \delta(p,0,0)=(q,\varepsilon)\) 第三步,转移到终结状态 $\delta(p,\varepsilon, z_0)=(r,z_0)$
图示如下,这是一个不确定的PDA
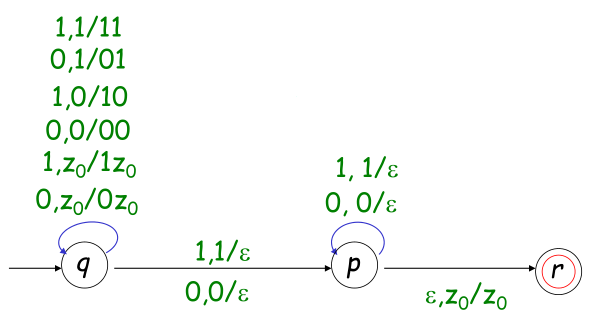
2 确定的PDA
如果一个PDA $P=(Q,\,\Sigma,\,\Gamma,\,\delta,\,q_0,\,z_0,\,F)$ 是确定的,那么它满足下面的条件:
- $\forall q\in Q,\forall a\in \Sigma \cup \{\varepsilon\},\forall X\in \Gamma$,$\delta(q,a,X)$ 的结果是唯一的;
- $\delta(q,a,X)$ 和 $\delta(q,\varepsilon ,X)$ 只能有一个有定义,因为对于状态$q$来说,读 $\varepsilon$ 意味着不读 $a$,而另一个意味着读 $a$,所以读与不读就产生了不确定性。
例:构造确定的PDA识别 $L = \{ 0^n1^n | n > 0 \}$
解:这就是一个DPDA
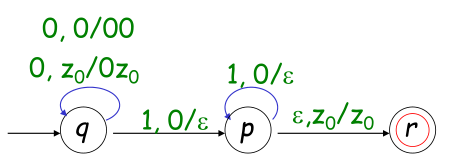
3 PDA的瞬时描述
用一个三元组 $(q,w,\alpha)$ 来描述一个PDA在某一时刻的格局,其中,
- $q$ 是PDA此时的状态;
- $w$ 是剩余的待读入字符串;
- $\alpha$ 是栈中的字符串。
例:用格局序列描述2中构造的 $L = \{ 0^n1^n | n > 0 \}$ 的PDA接受 $w=0011$ 的过程。
解:$(q,0011,z_0)┝(q,011,0z_0)┝(q,11,00z_0)┝(p,1,0z_0)┝(p,\varepsilon,z_0)┝(r,\varepsilon,z_0)$
简记为 $(q,0011,z_0)┝^* (r,\varepsilon,z_0)$
4 PDA接受的语言
能够由PDA接受(CFG构造)的语言称为上下文无关语言(CFL),PDA可以用两种方式描述接受语言:
- 用终结状态来描述:$L(P) = \{w\,|\, (q_0, w, z_0)┝^* (q, \varepsilon, \alpha), q\in F\}$
- 用空栈状态来描述:$N(P) = \{w\,|\, (q_0, w, z_0)┝^* (q, \varepsilon, \alpha)\}$
- 这两种描述方式是等价的,即 $L(P) \Leftrightarrow N(p)$
例如2中构造的 $L = \{ 0^n1^n | n > 0 \}$ 的PDA就是用终结状态接受的,也可用空栈状态来描述,如下
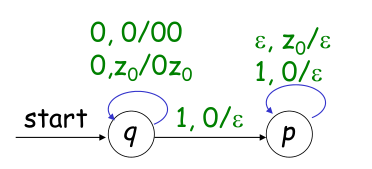
但是并不是所有的PDA都可以用两种方式构造 (针对DPDA),当 $L$ 可以被终结状态的DPDA接受并且 $L$ 有前缀性的时候,$L$ 才能被空栈状态的DPDA接受。
语言的前缀性:该语言中没有两个不同的字符串x和y,使得x是y的前缀。
如:语言 0* 就没有前缀性,因为0是00的前缀。
3 CFG和PDA的等价性
对于一个给定的上下文无关语言 $L$,存在一个CFG生成 $L$,且存在一个PDA识别 $L$。
1 CFG $\Rightarrow$ PDA
把CFG $G=(V,T,S,P)$ 转化为PDA,则对应的PDA为 $B=(\{q\},T,V\cup T,\delta,q,S,\{\,\})$,其中,
- $\delta(q, \varepsilon, A) =\{(q, \alpha ) | A\rightarrow \alpha \in P \}$
- $\delta(q, a, a) =(q, \varepsilon)$
例:将CFG $G=(\{S\},\{0,1\}, \{S\rightarrow 0S1, S\rightarrow SS, S\rightarrow \varepsilon \}, S)$ 转化为PDA。
解:PDA为 $P=(\{q\}, \{0,1\}, \{0,1,S\}, \delta, q, S, \{\,\})$,其中 $\delta$ 定义如下:
- $\delta(q,\varepsilon, S)=\{(q,0S1), (q,SS), (q,\varepsilon)\}$
- $\delta (q,0,0)=\{(q,\varepsilon )\}$
- $\delta (q,1,1)=\{(q,\varepsilon )\}$
用图表示
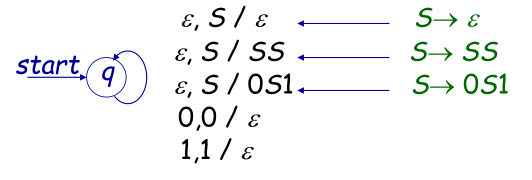
该PDA识别字符串 $w=0011$ 的过程:
$(q,0011,S)┝(q,0011,0S1)┝(q,011,S1)┝(q,011,0S11) ┝(q,11,S11)┝(q,11,11)┝(q,1,1)┝(q,\varepsilon,\varepsilon)$
对应的CFG派生序列:$S \Rightarrow 0S1 \Rightarrow 00S11 \Rightarrow 0011$
转化出的PDA实际上是在模拟CFG的派生过程,所以PDA一定能就识别CFG生成的字符串
2 PDA $\Rightarrow$ CFG
把PDA $P=(Q,\,\Sigma,\,\Gamma,\,\delta,\,q_0,\,z_0,\,F)$ 转化为CFG,则对应的CFG为 $G=(V,\Sigma,S,R)$,其中,
- $V$ :包括开始变元 $S$,这个变元和PDA没有关系,就是强行规定的;还有其他形如 $[qXp]$ 的符号,其中$\forall q,p \in Q, X\in \Gamma$
- 符号 $[qXp]$ 的意义是在 $q$ 状态下,可以使栈中的 $X$ 弹出并转移到 $p$ 状态的字符串,例如有状态转移函数 $\delta(q_0, \varepsilon, z_0) = (p, \varepsilon)$,则 $[q_0z_0p]\rightarrow \varepsilon$,于是对于下面 $R$ 的第一条产生式规则,就有$S\rightarrow [q_0z_0p]$
- $R$ :包括 $\forall p\in Q$,$S\rightarrow [q_0z_0p]$;还有 $[q X r_k]\rightarrow a[rY_1r_1][r_1Y_2r_2]… [r_{k-1}Y_kr_k]$,对于 $(r, Y_1Y_2…Y_k)\in \delta (q,a,X)$
- 第一条产生式规则已经在上一条中描述了,下面是关于第二条产生式规则。对于状态转移函数 $\delta(q, a, X) = (r,Y_1Y_2…Y_k)$,因为 $[qXr_k]$ 表示的是把 $X$ 全pop掉所需要的字符串,而状态转移函数读入字符串 $a$ 之后栈中的元素是 $Y_1Y_2…Y_k$,所以需要把这些元素也pop掉,因此最后的状态就不是 $r$ 而是 $r_k$,而第二条产生式规则的body部分 $a$ 之后的部分就是做这个的。
例:还是用 2.2确定的PDA 中的例子,将其转化成CFG

解:$P=(Q,\,\Sigma,\,\Gamma,\,\delta,\,q_0,\,z_0,\,F)\Rightarrow G=(V,\Sigma,S,R)$,其中 $V=\{S,[qz_0q], [qz_0p], [q0q], [q0p], [q1q], [q1p],[pz_0q], [pz_0p], [p0q], [p0p], [p1q], [p1p] \}$
然后根据转移函数导出产生式 $R$
- $\delta (q, 0, z_0) = (q, 0z_0)\Rightarrow [qz_0r_2]\rightarrow 0[q0r_1][r_1z_0r_2], \forall r_1,r_2\in Q \Rightarrow
[qz_0q] \rightarrow 0[q0q][qz_0q]\; |\; 0[q0p][pz_0q]
[qz_0p] \rightarrow 0[q0q][qz_0p]\; |\; 0[q0p][pz_0p]$ - $\delta (q, 0, 0) = (q, 00)\Rightarrow [q0r_2] \rightarrow 0[q0r_1][r_10r_2], \forall r_1,r_2\in Q \Rightarrow
[q0q] \rightarrow 0[q0q][q0q]\; |\; 0[q0p][p0q]
[q0p] \rightarrow 0[q0q][q0p]\; |\; 0[q0p][p0p]$ - $\delta(q, \varepsilon, z_0)=(p,z_0) \Rightarrow [qz_0r_1] \rightarrow [pz_0r_1], \forall r_1\in Q \Rightarrow
[qz_0q] \rightarrow [pz_0q]
[qz_0p] \rightarrow [pz_0p]$ - $\delta(q, 1, 0) = (p,\varepsilon) \Rightarrow [q0p] \rightarrow 1$
- $\delta(p, 1, 0) = (p,\varepsilon) \Rightarrow [p0p] \rightarrow 1$
- $\delta(p, \varepsilon, z_0) = (p,\varepsilon) \Rightarrow [pz_0p] \rightarrow \varepsilon$
把得到的产生式整合在一起得到 $R$ \(R = \\{\quad S \rightarrow [qz_0q]\,\, \|\,\, [qz_0p],\\ [qz_0q] \rightarrow 0[q0q][qz_0q] \,\,\|\,\, 0[q0p][pz_0q],\\ [qz_0p] \rightarrow 0[q0q][qz_0p] \,\,\|\,\, 0[q0p][pz_0p],\\ [q0q] \rightarrow 0[q0q][q0q] \,\,\|\,\, 0[q0p][p0q],\\ [q0p] \rightarrow 0[q0q][q0p] \,\,\|\,\, 0[q0p][p0p],\\ [qz_0q] \rightarrow [pz_0q],\;[qz_0p] \rightarrow[pz_0p],\\ [q0p] \rightarrow 1,\; [p0p] \rightarrow 1,\; [pz_0p] \rightarrow \varepsilon \quad\\}\) 最后把 $R$ 按如下规则化简一下:
- 消除含有没有终结符的变元的产生式,如:含有 $[pz_0q]$ 的产生式;
- 消除死循环的产生式,如:$[q0q]$ 的第一个产生式,因为它的第二个产生式由于 $[p0q]$ 满足第一条化简规则,所以它只剩下第一个产生式,所以它死循环了;
- 消除含有由于前两条规则导致的无用变元的产生式,如:因为 $[q0q]$ 无用,所以含有它的产生式也无用。
最终得到 \(R = \\{\quad S \rightarrow [qz_0p],\;[qz_0p] \rightarrow 0[q0p][pz_0p],\\ [q0p] \rightarrow 0[q0p][p0p],\; [qz_0p] \rightarrow[pz_0p],\\ [q0p] \rightarrow 1,\; [p0p] \rightarrow 1,\; [pz_0p] \rightarrow \varepsilon \quad\\}\) 看起来不太方便,于是令$A=[qz_0p], B=[q0p], C=[p0p], D=[pz_0p]$,得到
$R = \{ S \rightarrow A,\; A\rightarrow 0BD|D,\; B\rightarrow1|0BC,\; C\rightarrow1,\; D\rightarrow \varepsilon \}$
再次化简得到:$R = \{ S\rightarrow 0B|\varepsilon,\; B\rightarrow 1| 0BC,\; C\rightarrow1 \}$
4 上下文无关语言的性质
1 泵引理
上下文无关语言的泵引理:$L$ 是一个CFL,则 $\exist n$,对 $\forall w\in L$,若 $|w|\ge n$,则 $w$ 可以划分为 $w=uvxyz$,其中
- $|vxy| \le n$
$|vy| \ge 1$,(要是vy同时为空就出现 $A\rightarrow A$ 这种没有意义的产生式了)
- $uv^ixy^iz\in L,\;\,\forall i=0,1,2,…$
n的取法:令 $m=|V|$,$k=max\{ |\alpha| \forall A\rightarrow \alpha \}$,则 $n=k^m$
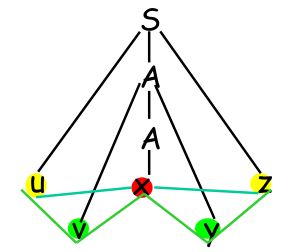
派生过程:$S\stackrel\Rightarrow uAz \stackrel\Rightarrow uvAyz\stackrel*\Rightarrow w$,语法解析树如下,对于重复出现的 A 来说,则可用子树的A代替父节点,此时失去的就是一对vy节点。
例:证明 $L=\{ww|w\in \{0,1\}^*\}$ 不是CFL。
解:假设L是CFL。则由泵引理可知,存在一个常数n,对于L中长度不小于n的字符串w就可以划分为五个部分,$w=uvxyz$,其中 $|vxy| \le n$,$vy \ne \varepsilon$,$uv^kxy^kz\in L$。
取 $w=0^n1^n0^n1^n\in L$,则 $uvxyz=0^n1^n0^n1^n$(如果要推出矛盾,就需要推出 $uxz\notin L$)。v和y不能同时为空串且 $|vxy| \le n$,所以它们的取值情况可以分为7种情况,这七种情况又可以分为两类:
- 第一类:vxy在同一类字符里,即同在开始的n个0、同时在开始的n个1里、同时在结束的n个0里,同时在结束的n个1里。这四种情况是等价的,而显然在第一种情况下有 $uxz\notin L$,因为开始的0的个数不足n了。
- 第二类:vxy在连续的两类字符里,即在前半部分的 $0^n1^n$ 中、在中间的 $1^n0^n$ 中、在后半部分的 $0^n1^n$中。这三种情况是等价的,而显然在第一种情况下有 $uxz\notin L$,因为开始的0和1的个数都不足n了。
所有的情况都推出了矛盾,所以假设错误,即 L 不是CFL。
2 封闭性
CFL在并、连接、星、反转、交、同态、逆同态运算下是封闭的,而在交、补运算下不是封闭的。
对于两个CFL $L_1$ 和 $L_2$,令 $G(L_1)=(V_1,T_1,R_1,S_1), G(L_2)=(V_2,T_2,R_2,S_2)$
- 并:$G(L_1 \cup L_2 ) = (V_1\cup V_2\cup \{S\},T_1\cup T_2, R,S)$,$R= \{S\rightarrow S_1 | S_2\} \cup R_1\cup R_2$
- 连接:$G(L_1 \cup L_2 ) = (V_1\cup V_2\cup \{S\},T_1\cup T_2, R,S)$,$R= \{S\rightarrow S_1 S_2\} \cup R_1\cup R_2$
- 星:$G(L_1^*) = (V_1,T_1, \{S_1\rightarrow S_1S_1|\varepsilon\}\cup R_1,S_1)$
- 反转:$G(L_1^R)=(V_1,T_1, \{A\rightarrow \alpha^R|A\rightarrow \alpha R_1\},S_1)$
交运算不封闭,例如:$L_1 =\{a^nb^nc^m | n\ge 0, m\ge 0\},\;L_2 =\{a^nb^mc^m | n\ge 0, m\ge 0\}$ 是两个CFL,它们的交就是 $L_1 \cup L_2 =\{ a^nb^nc^n | n\ge 0\}$,这不是CFL,可以按照上面的方式用泵引理证明。
但是一个CFL和一个RL做交运算之后得到的还是CFL,这个条件下它是封闭的。