1 形式化定义
图灵机(Turing Machine):TM是一个七元组$P=(Q,\,\Sigma,\,\Gamma,\,\delta,\,q_0,B,\,F)$,其中,
- $Q$ 是有限的状态集;
- $\Sigma$ 是有限的输入字符集;
- $\Gamma$ 是有限的纸带字符集;
- $\delta$ 是状态转移函数,是一个映射 $Q\times \Gamma \Rightarrow Q\times \Gamma \times {R,L}$,状态转移函数 $\delta(q, X ) = (p, Y, D)$ 表示状态从q到p,读写头所指的字符X被改为Y,读写头向D方向移动;
- $q_0$ 是初始状态;
- $B$ 是空格符,一个特殊的符号;
- $F$ 是终结状态集;
例:构造TM识别 $L = { a^nb^nc^n | n \ge 0 }$
初始状态:
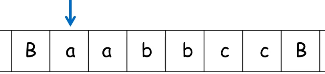
最终状态:
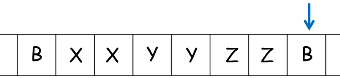
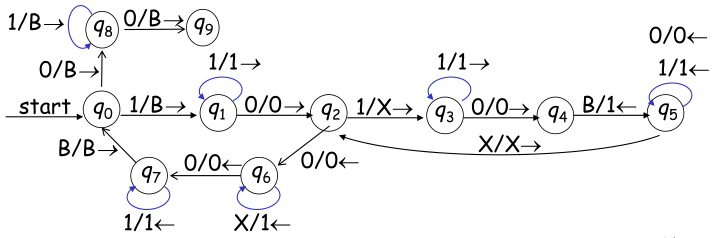
构造的图灵机:$M=({q_0,q_1,q_2,q_3,q_4},{a,b,c},{a,b,c,B,X,Y,Z},\delta, q0,B,{q_4})$
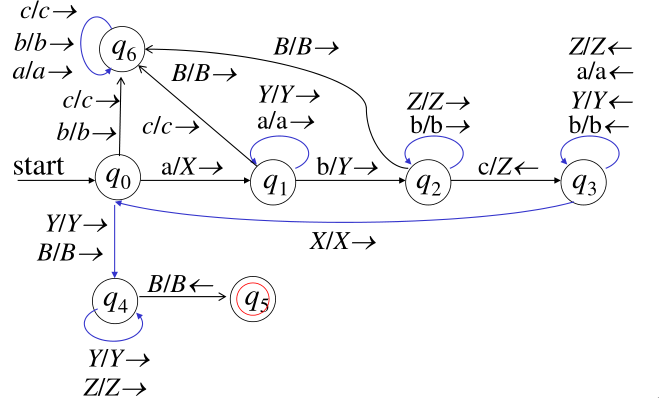
上图表示的是确定的图灵机,删除 $q_6$ 得到的是不确定的图灵机,也可以识别语言 L
1 瞬时描述
用 $X_1… X_{i-1}qX_i X_{i+1}…X_n$ 的形式表示图灵机在某一时刻所处的格局,q表示图灵机所处的状态,读写头指向的位置为状态符q右侧的字符,即 $X_i$ 。
如上的图灵机识别字符串 $aabbcc$ 的过程描述如下:$q_0aabbcc┝Xq_1abbcc┝ Xaq_1bbcc┝XaYq_2bcc XaYbq_2cc┝X aYq_3bZc┝X aq_3YbZc┝Xq_3aYbZc┝q_3XaYbZc┝Xq_0aYbZc┝XXq_1YbZc┝XXYq_1bZc ┝ XXYYq_2Zc┝XXYYZq_2c┝XXYYq_3ZZ┝…┝XXYYZZq_3$
2 停机
读了某个字符X之后,图灵机仍在状态q,不做任何动作,没有进行状态转移,简言之就是在状态q读入X没有相应的状态转移函数 。
- 不知道读写头向左/右移动;
- 不知道X应该被改成什么;
- 不知道转移到哪个状态;
2 构造
例:设计一个TM计算两个正整数x和y的和,即 x+y。
思路:用x个1表示x,用y个1表示y,中间用0分隔。运算过程为,从左到右移动读写头,经过0则把它改成1,右移到B则左移一次,把1改成B,结束。状态转移图如下:
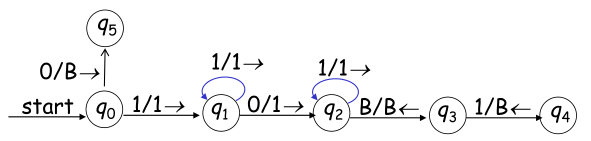
例:设计TM计算 $f(w)=ww,w\in {1}^+$ 。
思路:用0分隔原来的w和复制得到的w,读一个1写一个1,并把读过的1改成X,复制结束后把X改回1,最后把左边的1右移一格,或者把右边的1左移一格即可(使用上题的方式)。
例:设计TM计算 $f(w)=ww,w\in {0,1}^+$ 。
思路:用字符A分隔原来的w和复制得到的w,用状态表示所读的是1还是0,读0则到q0状态,读1则到q1状态,然后根据所处的状态决定是写0还是写1。其余的参照上题的思路。
例:设计一个TM计算两个正整数m和n的积,即 m×n。
思路:做m个n相加,每加一个n,抹掉一个m的1,直到m的1全部被抹除。最后把与结果无关的全都抹除。
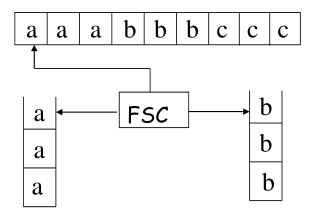
3 双栈自动机 (Two Stack Machine)
状态转移函数:$\delta(q, a, X , Y ) = (p, \alpha, \beta)$ 图示:
例:构造双栈自动机识别 $L={a^nb^nc^n| n\ge 0}$
解:就是把所有的a先压栈,读b把b压栈的同时将a弹栈,最后用c把b弹栈
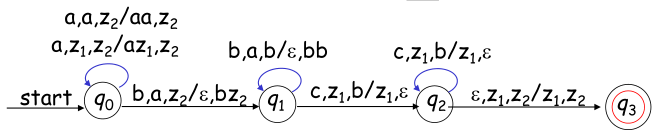
4 图灵机编码
1 字符串排序枚举
对 $w\in {0,1}^*$ 按照长度排序:$\varepsilon,0,1,00,01,10,11,000,001,010,011,…$
把上面的每个字符串前面用1连接得到:$1,10,11,100,101,110,111,1000,1001,1010,1011,…$
则可发现,若把 $1w$ 视为二进制数,则如果 $w$ 是第 $i$ 个字符串就有 $1w=i$
2 编码
对于TM $M = (Q, {0,1}, \Gamma, \delta, q_1, B, {q_2})$,其中 $Q ={q_1,q_2, …,q_r}$,$\Gamma={X_1,X_2,X_3, …,X_s}$,并规定 $X_1=0, X_2=1,X_3=B,D_1=L,D_2=R$,$q_1$ 是初始状态,$q_2$ 是终结状态。
将转移函数编码为:$\delta (q_i, X_j) = (q_k, X_m, D_n)\Rightarrow 0^i10^j10^k10^m10^n$。用 1 隔开
则M可编码为:$C_111 C_211 C_311 … C_{n-1}11 C_n$,其中的 $C_i$ 表示状态转移函数的编码。用 11 隔开
$C_i$ 之间是无序的,所以一个TM可以有不同的编码
例:编码如下TM
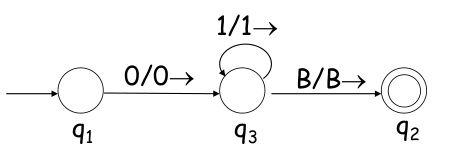
解:$\delta(q_1,0)=(q_3,0,\rightarrow) \Rightarrow 010100010100\ \delta(q_3,1) =(q_3,1,\rightarrow)\Rightarrow 0001001000100100\ \delta(q_3,B) =(q_2,B,\rightarrow)\Rightarrow 00010001001000100$
故 $TM \Rightarrow 010100010100 \;11\; 0001001000100100 \;11\; 00010001001000100$
因为图灵机编码成了01字符串,而01字符串是可以枚举的,于是我们就可以称被编码的图灵机为第 i 个图灵机,记为 $M_i$ 。
5. TM接受的语言
1 递归可枚举语言
能够由图灵机接受的语言称为递归可枚举语言(recursively enumerable language):$L={w\;|\; q_0w┝^* \alpha p\beta,\; p\in F,\; \alpha,\;\beta\in \Gamma^*}$
所有的正则语言都是递归可枚举语言,所有的上下文无关语言都是递归可枚举语言。
2 非递归可枚举语言
定理:$L_d={ w_i \;|\; w_i \in L(M_i) }$ 就是一个非递归可枚举语言(not-recursively enumerable language),即没有TM接受它。
证明:假设 $L_d$ 是以一个TM $M$ 的接受的语言 $L(M)$,则我们可以假设 $M$ 的编码为 $w_i$ ,即 $M=M_i$ 。然后判断 $w_i$ 是否在 $L_d$ 里:
- $w_i \in L_d$:由假设可知,$M_i$ 接受 $L_d$,则一定接受其中的每个字符串,可得 $M_i$ 接受 $w_i$,由 $L_d$ 定义进而得 $w_i \notin L_d$;
- $w_i \notin L_d$:由假设可知,$M_i$ 接受的是 $L_d$,由于 $w_i \notin L_d$ 则 $M_i$ 不接受 $w_i$,由 $L_d$ 定义进而得 $w_i \in L_d$;
所以推出矛盾,假设错误。
3 递归语言
如果存在TM $M$ 接受 $L$ 且满足下面两个条件,则称 $L$ 是递归语言 (Recursive languages)。
- $w \in L\Rightarrow M$ 接受 $w$ 并停机 (停在终结状态);
- $w \notin L\Rightarrow M$ 停机 (停在非终结状态);
定理:如果 $L$ 是递归语言,那么 $\overline L$ 也是。
证明:假设 $L=L(M), M=(Q,\,\Sigma,\,\Gamma,\,\delta,\,q_0,B,\,F)$,令 $\overline M=(Q\cup{r},\,\Sigma,\,\Gamma,\,\delta,\,q_0,B,\,{r})$,其中
- r 是一个新的状态,不在Q中;
- 对于任意的 $q\in Q-F$ 和 $a\in \Sigma$,如果 $\delta(q,a)=\phi$,则有 $\delta(q,a)=(r,a,\rightarrow)$;
定理:如果 $L$ 和 $\overline L$ 都是递归可枚举语言,那么 $L$ 就是递归语言。
证明:假设 $M_1=(Q_1,\,\Sigma,\,\Gamma,\,\delta_1,\,q_1,B,\,F_1), M_2=(Q_2,\,\Sigma,\,\Gamma,\,\delta_2,\,q_2,B,\,F_2)$ 分别接受 $L$ 和 $\overline L$,则令 $M = (Q_1\times Q_2, \Sigma,\,\Gamma, \delta, (q_1,q_2), B, F_1\times (Q_2-F_2)),\delta((q,a),(a,b))=(\delta_1(p,a),\delta_2(q,b))$ 即可用递归的方式接受 $L$ ,也就是读 $L$ 中的 $w$ 停在终结状态,读 $\overline L$ 中的 $w$ 停在非终结状态。
这个定理证明的时候构造的是一个有两个tape的图灵机。
4 通用语言
一个语言 $L$ ,它是递归可枚举的但不是递归的,即如果 $w\in L$ 则对应的 $M$ 接受它,但如果 $w\notin L$ 则 $M$ 不接受它且不会停机,则称它为通用语言 (Universal language)。$L_u = { (M,w) | w \in L(M) }$ 就是一个通用语言,其中 $M$ 是对应图灵机的编码,$w$ 是图灵机接受的字符串,连接成 $Mw$,记为 $(M,w)$。
通用图灵机:四条tape,以 $L(M) = {0}{1}^*$ 为例
- Tape1:图灵机的编码+111+接受的字符串;例:010100010100 11 0001001000100100 11 00010001001000100 111 011
- Tape2:接受的字符串编码;例:10100100,以1开头,用一个0表示0,两个0表示1
- Tape3:图灵机的状态;例:0,用0的个数表示状态
- Tape4:模拟图灵机的处理过程;
5 语言的范畴
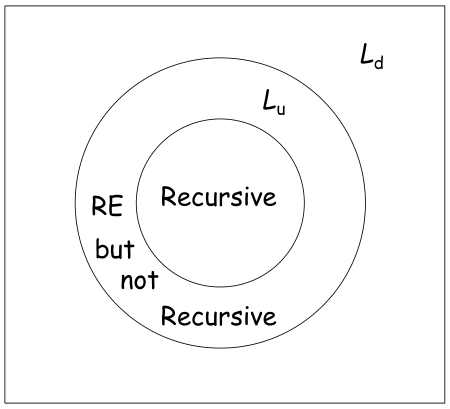
6 乔姆斯基文法
乔姆斯基文法一共分为四型:
Type 0:短语文法 phrase structure grammar(PSG) —— 没有任何约束
$\quad\alpha \rightarrow \beta;\;\; \alpha\in(V\cup T)^V (V\cup T)^, \beta\in(V\cup T)^*$
Type 1:上下文有关文法 context sensitive grammar(CSG) —- A左右为约定的字符串
$\quad\alpha A\beta \rightarrow \alpha\omega\beta;\;\; A\in V,\; \alpha,\omega,\beta\in(V\cup T)^*$
Type 2:上下文无关文法 context free grammar(CFG) —- A左右都为空串
$\quad A\rightarrow \omega;\;\; A\in V,\;\omega\in(V\cup T)^*$
Type 3:正则文法 regular grammar(RG) —- A只能生成终结符或有一个变元且都在左(右)侧的式子
右线性文法 $A \rightarrow \alpha|\alpha B;\;\; A,B\in V,\;\alpha\in T^$ 或左线性文法 $A \rightarrow \alpha|B\alpha;\;\; A,B\in V,\;\alpha\in T^$
上下文有关文法对应上下文有关语言和线性有界自动机 (把图灵机中的空格符用 “[” 和 “]” 替换,处理的过程中读写头不能越过它们限定的范围)。